A. Les bases du problème
a) La découverte de la pyramide
b) Le théorème en lui-même
B. Les moyens utilisés pour la mesure de la pyramide
C. La mesure de la pyramide
Conclusion
Sources
Annexes
J’ai choisi de raconter une histoire, une histoire ayant trait aux mathématiques. Plus précisément, je vais vous narrer l’histoire de la naissance et de la construction d’un théorème célèbre dont le nom de l’inventeur lui est lié : le théorème de Thalès.
A priori, les mathématiques ont plutôt une image négative, elles paraissent être une science austère parce que tributaire d’une nécessité d’exactitude. Nécessité qui les conduit à vouloir être exactes en tous temps et en tous lieux, donc à demeurer éternellement vraies.
Mais, il faut dépasser cette opinion et redonner une image positive aux mathématiques, bref les réconcilier avec la vie. Ne serait-ce que pour comprendre pourquoi certains hommes brûlent la leur à tenter de résoudre des énigmes mathématiques.
Pour cela il faut redonner aux mathématiques leur place dans l’histoire de la construction des savoirs et montrer en quoi celles-ci ont contribué à la naissance de la pensée.
Afin de répondre à ce problème, nous allons retourner aux sources de l’apparition de cette science, à savoir l’Antiquité Grecque au sein de laquelle Thalès de Milet compte parmi les figures les plus éminentes de son temps. Nous allons donc raconter l’histoire du célèbre théorème de Thalès afin de vous démontrer que les mathématiques peuvent être passionnantes et vivantes.
I. Thalès de Milet : Le personnage.
Thalès naquit et vécut vers –620 avant JC sur les côtes de l’Anatolie en Ionie dans la ville de Milet, cité portuaire et centre d’un commerce étendu aux deux bassins de la méditerranée. Il mourut âgé d’environ 90 ans (-547) en assistant à des jeux gymniques, pressé par la foule et épuisé de chaleur.
Ce riche commerçant était un homme à multiples facettes qui a acquit de son vivant une réputation d’homme d’Etat, d’ingénieur, d’affaire ; mais aussi de philosophe, de mathématicien et d’astronome.
Sa réputation d’astronome tient à ce qu’il a rendu compte que l’année dure 365 jours ; à ce qu’il est le premier à découvrir la trajectoire du Soleil d’un solstice à un autre ; le premier à découvrir la petite Ourse ; le premier à déterminer la taille et la nature du Soleil.
Mais ce qui lui valut de rester célèbre fut sa prédiction de l’éclipse du Soleil (-585), alors qu’il avait une quarantaine d’années, prédiction rendue possible par des connaissances en astronomie suffisamment fiable pour faire des prédictions rationnelles.
Thalès s’est aussi distingué par son génie militaire : il aurait détourné le cours d’une rivière pour faire passer l’armée du roi de Lydie.
C’est aussi le premier spéculateur de l’Histoire. En effet, une année, la récolte d’olive étant abondante, Thalès acheta toutes celles produites dans le district, il les écoula petit à petit, ce qui évita la chute des prix et lui rapporta d’énormes profits.
Mais dans un même temps, Thalès occupe une place primordiale dans l’histoire de la philosophie. En effet, il n’est autre que le premier « penseur » de l’Histoire grecque, c’est-à-dire le premier à s’être posé des questions (« Qu’est–ce que penser ? », « Est-ce qu’il y a des choses qui échappent à ma pensée ? », « De quoi est faite la nature ? »…). C’est donc le premier philosophe de l’Histoire, en d’autres termes le premier à tenter de donner une explication systématique et rationnelle du monde. Explication qu’il applique aussi aux mathématiques : il est le premier à énoncer des résultats généraux concernant les objets mathématiques. Avant lui, on ne s’intéressait qu’à la résolution de problèmes particuliers. L’apparition de théories universelles est une nouveauté absolue, quand on dit : « Toute droite passant par le centre d’un cercle le coupe en deux parties égales », c’est une réelle innovation. C’est pour cela que Thalès est considéré comme le premier mathématicien de l’Histoire. D’ailleurs, à son époque (VII siècle avant JC), les termes « philosophie » et « mathématique » n’existaient pas encore, ils formaient alors un tout, ils étaient imbriqués l’un dans l’autre avant d’être séparés bien plus tard.
C’est pourquoi Thalès est considéré à la fois comme le Père de la physique ionienne et comme le Père de la philosophie. C’est le premier des grecs à découvrir la géométrie, à montrer envers la nature une certaine curiosité scientifique et à observer les astres avec beaucoup de compétence.
Toutefois, malgré l’étendue de tout son savoir, si le nom de Thalès résonne encore dans nos oreilles, au XXIe siècle, c’est pour le théorème associé à son nom : le théorème de Thalès.
II. La construction du théorème.
A. Les bases du problèmes.
a) La découverte de la pyramide de Khéops.
Son activité de commerçant l’ayant enrichi, Thalès de Milet put consacrer la fin de sa vie aux études et aux voyages. Son premier périple le mena en Egypte. Là, il calcula la hauteur des pyramides grâce à leur ombre portée : c’est une première utilisation du théorème qui porte son nom.
Nous nous proposons, ici, d’expliquer pourquoi ce théorème a vu le jour, de déterminer ce qui est à l’origine de sa découverte, dans quelles circonstances elle a été rendue possible ; bref nous tâcherons de remonter aux causes premières, au « déclic de génie » qui mène à l’élaboration d’un théorème universel.
Au cours de son voyage en Egypte, Thalès de Milet tomba en béatitude devant l’immensité de la pyramide de Khéops : les dimensions du monument dépassent l’imagination, lui font sentir sa petitesse, la pyramide est hors norme, sans commune mesure et apparemment immesurable. L’édifice pourtant construit par des hommes restait hors de portée de leur connaissance : la hauteur de la pyramide était impossible à mesurer.
Mesurer l’immesurable : voilà le défi que Thalès se propose de relever.
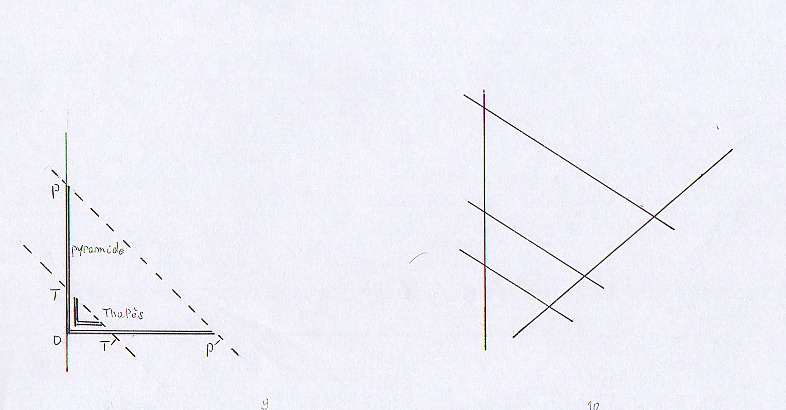
Il trouve un allié dans sa quête : le Soleil. Pourquoi le Soleil ? Parce qu’il traite toutes les choses du monde de la même façon, et en traitant semblablement l’Homme minuscule et le gigantisme de la pyramide, le Soleil établit la possibilité d’une commune mesure.
Ce qui signifie que le rapport que j’entretiens avec mon ombre est le même que celui que la pyramide entretient avec la sienne, de ceci découle qu’à l’instant où mon ombre est égale à ma taille, l’ombre de la pyramide est égale à sa hauteur.
Thalès emploie ici une ruse : il va obtenir le vertical par l’horizontal (par l’ombre écrasée au sol). Avec le petit, il va mesurer le grand ; avec le proche, mesurer le lointain.
Ce raisonnement nous montre que les mathématiques sont une ruse de l’esprit.
b) Le théorème en lui-même.
Avant toute chose, rappelons ce qu’est le théorème de Thalès.
ANNEXE 1
Sur un couple de données D et D’, une série de parallèles AA’, BB’, CC’, découpe des segments qui sont en proportion.
Ce théorème est révolutionnaire car avec lui débute la science des proportions, d’ailleurs le théorème de Thalès est également appelé le théorème des proportions. En d’autres termes, toutes les figures semblables ont la même forme ; conserver les proportions c’est conserver la forme (la forme est ce qui se conserve quand on garde les proportions et que l’on change les dimensions).
Mais concrètement, que nous dit le théorème de Thalès, quel est son apport ? Questionnons ce théorème : dire que « AB est égale à A’B’ ce que AC est à A’C’ » c’est dire que le premier couple et le second sont dans le même rapport, ce qui signifie que ce théorème génère toutes les questions qui mettent en jeu les rapports :
* Changements d’échelles
* Modèles réduits
* Plans
* Cartes
* Réductions / aggrandissements
Ce théorème a une utilité pratique, il est une véritable innovation.
B. Les moyens utilisés pour la mesure de la pyramide.
Ce qui est intéressant alors est de savoir comment Thalès a procédé concrètement à l’aide du théorème pour mesurer cette pyramide ?
Ici, la difficulté est due à la figure pyramidale, à sa forme évasée :
* La pyramide de Khéops a une base carrée, et son axe tombe exactement au milieu du carré.
* La hauteur de la pyramide, c’est la longueur de l’axe.
* La longueur de l’ombre de l’axe, c’est la longueur de l’axe.
ANNEXE 2
Le problème qui se pose est que Thalès ne peut mesurer concrètement que la partie s’étendant en dehors de la base (puisque l’autre est à l’intérieur du monument, donc inaccessible).
Mais Thalès a trouvé une parade pour contourner la difficulté : en faisant sa mesure au moment où les rayons du Soleil étaient exactement perpendiculaires au côté de la base (c’est-à-dire quand la partie cachée était égale à la moitié d’un côté). Donc la hauteur de la pyramide sera égale à la hauteur de l’ombre + à la moitié d’un côté.
Afin de mieux comprendre, imaginons une pyramide transparente.
ANNEXES 2 et 3.
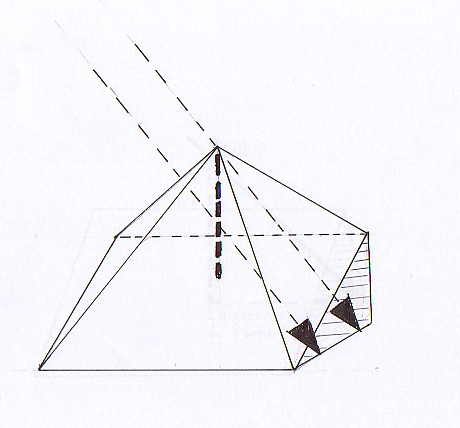
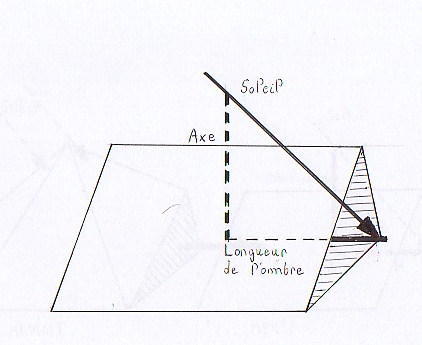
Sur une pyramide transparente, voici l’ombre de l’axe dont Thalès voulait déterminer la longueur.
ANNEXE 4.
(La partie de l’ombre en pointillé est inaccessible).
Tout ce que peut mesurer Thalès est la partie en gras, c’est la seule information dont il dispose.
ANNEXE 5.
C’est une simple opération de l’esprit : Thalès a oublié la masse du monument, il en a fait abstraction.
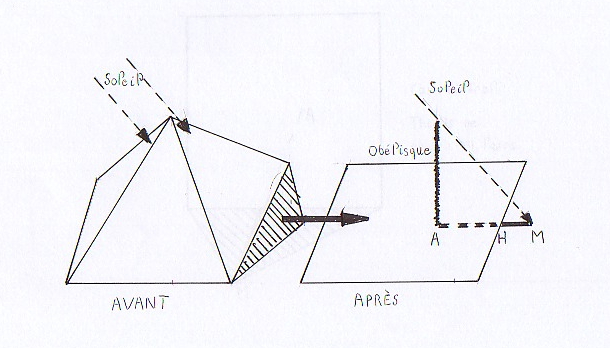
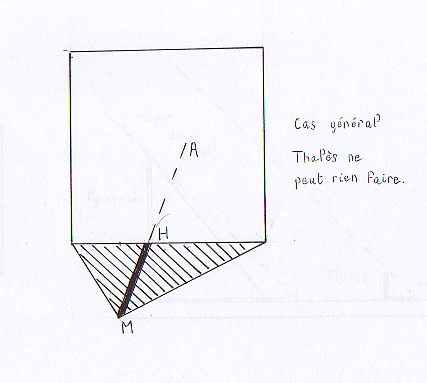
Toutefois, l’explication théorique aussi simple qu’elle peut paraître se confronta aux aléas de la pratique, à des difficultés extérieures. En effet, la démonstration du théorème va dépendre des rayons du soleil : la plupart du temps, la direction des rayons du soleil faisait un angle quelconque avec le côté de la base et Thalès ne pouvait alors rien mesurer.
ANNEXE 6.
C. La mesure de la pyramide.
Mais les mathématiques sont une ruse : Thalès va rechercher une situation particulière. Il va résoudre son problème à un moment particulier de la journée, celui où les rayons sont perpendiculaires à la base.
Ce que Thalès ne pouvait atteindre par la mesure directe, il allait le déduire par le raisonnement. Quelles étaient ses armes ?
De la pyramide il ne connaît qu’une seule chose, le côté de la base. Il allait s’en servir.
ANNEXES 7 et 8.
Pourtant une question gênante subsiste : comment Thalès pouvait-il savoir que l’ombre était perpendiculaire au côté ?
Grâce à l’orientation de la pyramide : les architectes avaient construit le monument de façon à ce qu’une des faces soit orientée plein sud. Ainsi, l’ombre est perpendiculaire au côté au moment où le soleil est à son zénith, soit à midi pile.
Mais la mesure n’a pas été si simple à réaliser, en effet, la pyramide ne fait pas une ombre tous les jours de l’année à midi ! Le succès de l’expérimentation se trouve différé en raison d’aléas climatiques (les nuages qui masquent le soleil). Pour réussir cette entreprise, il faut que toutes les conditions soient réunies. Thalès doit opérer de manière empirique.
Dans ce cas précis, deux conditions sont à réunir :
* Que l’ombre soit égale à la pyramide.
* Que l’ombre soit perpendiculaire à la base.
Et pour répondre à ces conditions, il faut sortir du domaine de la géométrie pure et effectuer un travail de terrain. Aussi stupéfiant que cela puisse paraître, le mathématicien est aussi un homme de terrain.
Le travail de terrain, dans le cas de la pyramide de Khéops n’a pas été sans difficulté. En effet, celle-ci est érigée à Gizeh à 30° de latitude de l’hémisphère Nord, au dessus du tropique, et dans ces conditions géographiques, pour que l’ombre soit égale à l’objet, il faut que les rayons soient inclinés à 45°. Or en été, à midi, à Gizeh, le rayons sont presque verticaux, il n’y a donc pas d’ombre du tout durant cette période de l’année.
Une condition supplémentaire vient se greffer à la réalisation de la mesure : pour que l’ombre soit perpendiculaire à la base, elle doit être orientée Nord-Sud.
Et le remplissage de ces conditions ne sont réunies que deux jours dans l’année !!!
D’après les calculs d’astronomes, ces deux jours n’ont pu tomber qu’un 21 novembre ou un 20 janvier, soit en hiver et à l’ombre (le pauvre Thalès a du attraper froid avec le vent). On prend donc conscience, ici, qu’avant d’aboutir à un théorème général et universel, le théoricien doit se faire praticien et se conformer à des mesures particulières.
Ce qu’il nous reste à savoir maintenant, c’est combien mesure effectivement cette pyramide. Le seul instrument de mesure à disposition de Thalès était une corde. Il lui fallait donc une unité de mesure : il utilisera le Thalès, sa propre taille.
Il trouva 18 Thalès d’ombre, puis il mesura le côté de la base, divisa par deux et trouva 67 Thalès.
La pyramide de Khéops mesure donc 85 Thalès, soit 147 mètres (sachant qu’un Thalès valait 3,25 coudées égyptiennes ; 276,25 coudées au total). Par comparaison : la pyramide du Louvre mesure 21,60 mètres de hauteur et 34,40 mètres de côté, la Tour Eiffel mesure 320 mètres (la pyramide de Khéops fait donc environ la moitié de celle-ci).
J’ai voulu, à travers cet exposé, dépasser l’idée selon laquelle les mathématiques seraient une science désintéressée, cultivée pour elle-même, un pur exercice de raisonnement abstrait avec pour seule finalité le profit intellectuel.
J’ai au contraire insisté sur le côté pratique de cette science, et montré avec l’exemple de Thalès de Milet que l’un des apports essentiels des mathématiques grecques consiste en l’application de la géométrie dans des domaines pratiques.
Plus fondamentalement, il s’agissait de se souvenir qu’à l’origine de toute théorie mathématique il y a une démarche créative suivie d’une série d’expérimentations et de vérifications d’hypothèses. Mais aussi que cette démarche empirique a contribué (au même titre que la philosophie) à la naissance et à la construction des savoirs dans le bassin méditerranéen.
Le théorème du perroquet, Denis Guejd (Points)
Des mathématiciens de A à Z, Bertrand Hauchecorne et Daniel Surreau (Ellipses)
Penseurs Grecs avant Socrate, « De Thalès de Milet à Prodicos » (GF-Flammarion).
Vie, doctrines et sentences des philosophes illustres, Tome I, Diogène Läerce (GF-Flammarion)
Article sur Thalès de Milet dans L’Encyclopédia Universalis.
Annexe 1
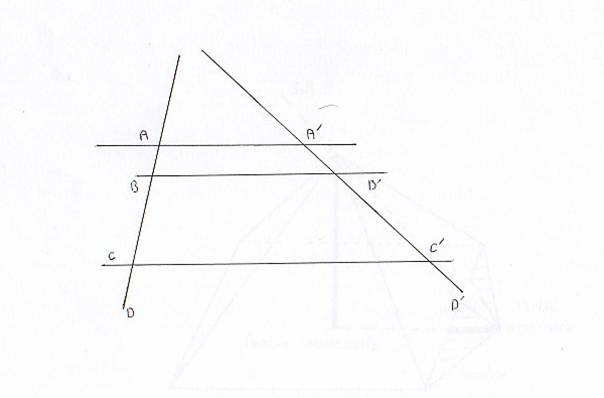
Annexe 2
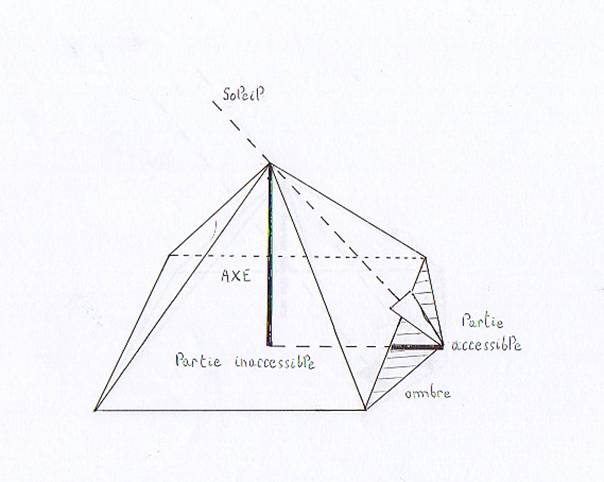
Annexe 3
Annexe 4
Annexe 5
Annexe 6
Annexe 7

Annexe 8